Describe in Words What This 2d Transformmatrix Does
Explain types of 2-D Transformation. 0 1 0 -1 0 0 1 1 1 In addition separate this matrix into the product of two matrices such that the function of each matrix and the ordering of the matrices correspond to your description above.

2 D Fourier Transforms Matlab Simulink
Write down the 33 matrix that rotates a 2D point by angle θ about a point p xp yp.

. Eñ be a basis for U. PDF represents its contents in a two-dimensional coordinate system. CSS 2D Transform Methods.
In this case which means that the graph is not shifted to the left or right. The horizontal shift depends on the value of. Coordinates of every point can be represented as a vector.
In other words the surface is treated as the image plane. When a transformation takes place on a 2D plane it is called 2D transformation. The actual meaning of transformations is a change of appearance of something.
One way to create the shadow of an object onto a surface eg the floor is to place an imaginary camera at the light source and then calculate the projection of the object onto that surface. For each xy point that makes up the shape we do this matrix multiplication. OpenGL does not provide shadows.
Describe the Transformation The transformation being described is from to. In some practical applications inversion can be computed using general inversion algorithms or by. In OpenGL vertices are modified by the Current Transformation Matrix CTM 4x4 homogeneous coordinate matrix that is part of the state and.
Square mp scale 2. Tait-Bryan vs Proper Euler. The two images shown in Figure 2 a and b have similar histograms see Figure 2 c and d.
FUNCTION AND ORDERING OF TRANSFORMATION MATRICES Describe in words what this 2D transform matrix does. Our first theorem formalizes this fundamental observation. We next define a J monad scale which produces the scale matrix.
We can have various types of transformations such as translation scaling up or down rotation shearing etc. Thismonad is applied to a list of two scale factors for and respectively. However while we typically visualize functions with their graphs people tend to use the word transformation to indicate that you should instead visualize some object moving stretching squishing etc.
A transformation matrix allows to alter the default coordinate system and map the original coordinates x y to this new coordinate system. Rotation about z x and z Note. Other words a linear transformation is determined by specifying its values on a basis.
Describe in words what this 2D transform matrix does. How does it work. Find the 3 by 3 matrix that create a 2D reflection about a line y mx c.
Tait-Bryan rotations rotate about three distinct axes x y z Proper Euler angles share axis for first and last rotation z x z Both systems can. Its domain and codomain are both R n and its range is R n as well since every vector in R n is the output of itself. The following methods are hard to read because instead of using meaningful names for the variables and methods they use names of fruit.
0 0 1 1 1 0 1 0 1 7. When the transformation matrix abcd is the Identity Matrix the matrix equivalent of 1 the xy values are not changed. When A is an invertible matrix there is a matrix A 1 that represents a transformation that undoes A since its composition with A is the identity matrix.
Figure 2 f shows that the neighboring pixels. The word transformation means the same thing as function. 1 Draw a line from the centre of enlargement to each vertex corner of the shape you wish to enlarge.
2 If the scale factor is 2 draw a line from the centre of enlargement through each vertex which is twice as long as the length you measured. Often a sequence like x y z is used. Matrix nnnnnn Defines a 2D transformation using a matrix of six values.
The purpose of this exercise is to practice reading code and recognizing the traversal patterns in this chapter. In other words the matrix of the combined transformation A followed by B is simply the product of the individual matrices. 0 1 0 -1 0 0 1 1 1 In addition separate this matrix into the product of two matrices such that the function of each matrix and the ordering of the matrices correspond to your description above.
Linear Algebra and geometry magical math Frames are represented by tuples and we change frames representations through the use of matrices. The output is the same as the input. In other words the identity transformation does not move its input vector.
After that the shape could be congruent or similar to its preimage. Changing the b value leads to a shear transformation try it above. TranslateX n Defines a 2D translation moving the element along the X-axis.
Theorem 51 Let U and V be finite-dimensional vector spaces over F and let eè. Translate xy Defines a 2D translation moving the element along the X- and the Y-axis. The horizontal shift is described as.
Example A real-word transformation. Transformation means changing some graphics into something else by applying rules. Something which takes in a number and outputs a number like.
Monad def 2 2 0 y001 y scale 2 32 00 3. Write down the 44 rotation matrix that takes the orthonormal 3D vectors u xu yu zu v xv yv zv and w xw yw zw to orthonormal 3D vectors a xa ya za b xb yb zb and c xc yc zc So Mu a Mv b and Mw c. Find the 4 by 4 matrix that rotates a rigid body by θaround the point xp 0zp and about the y-axis.
M is an nn orthogonal matrix if the transformation M preserves length that is Mx x r r. Measure the lengths of each of these lines. - The graph is shifted to the left units.
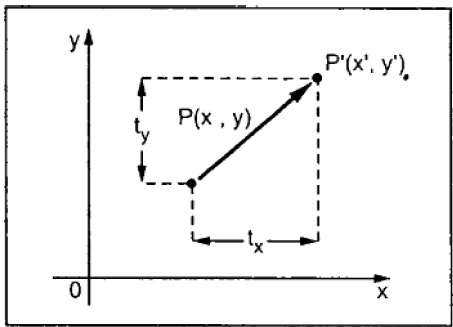
A point is essentially the multiplication of two matrices one describing the points coordinates and the other describing unit. A point in 2D space is going to be represented using matrices. Figure 2 f and g show the normalized autocorrelation among pixels in one line of the respective images.
Describe in words what this 2D transform matrix does. What is a transformation matrix. If a shape is transformed its appearance is changed.
We can now scale the square of Figure 1by. - The graph is shifted to the right units. Rotate about x axis then y axis then z axis But any sequence works.
There are basically four types of transformations.

How To Calculate The 2d Transformation Matrix Between Two Triangles In Javascript Stack Overflow
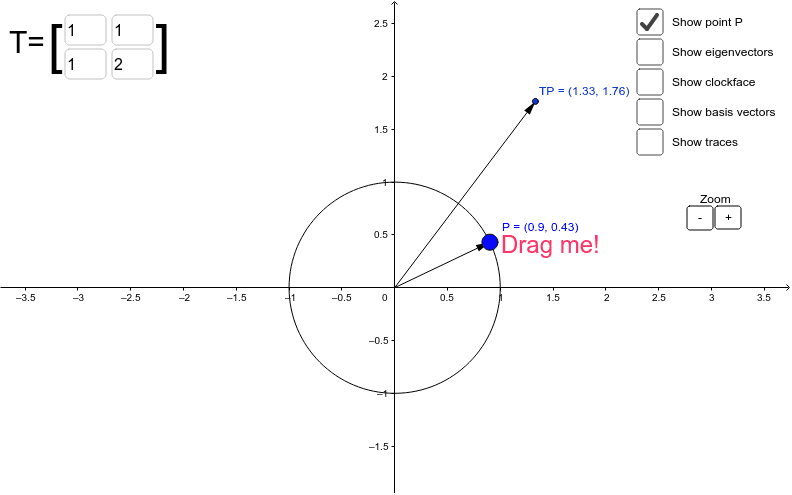
Linear Transformations And Eigenvectors In 2d Geogebra

Css3 Series Part 6 2d Transformation With Css3

Css3 Series Part 6 2d Transformation With Css3

Css3 Series Part 6 2d Transformation With Css3

2d Shape Word Mat 2d Shapes Names 2d Shapes Shape Names

2d Shapes Number Of Sides 2d Shapes Shape Posters 2d Shapes Names

2d Shape Word Mat An Attractive Word Mat Featuring All The Common 2d Shape Names And Accompanying Pictures A Great Aid 2d Shapes 2d Shapes Names Shape Names

2d Transformation Methods In Css
![]()
The Perspective And Orthographic Projection Matrix What Are Projection Matrices And Where Why Are They Used

Solved 2 Commutativity Of Transforma Tion Matrices 25 1 Chegg Com

2d Transformation Methods In Css

Solved Function And Ordering Of Transformation Matrices Chegg Com
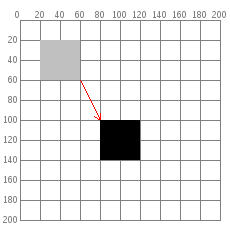
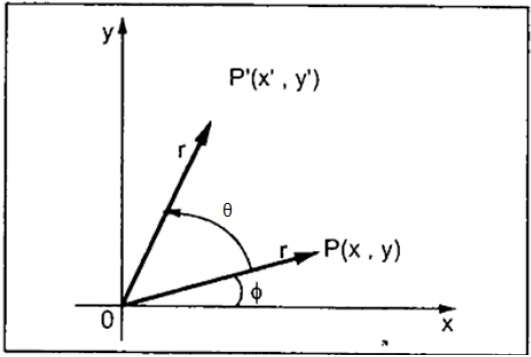
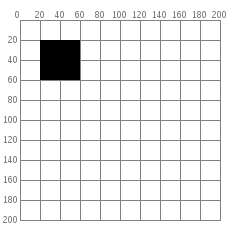

Comments
Post a Comment